Introducción
Esta y subsecuentes entradas de blog, bajo la categoría de “redes neuronales”, se ocuparán de explicar algo de la teoría matemática básica de las redes neuronales artificiales; qué es una red neuronal y los componentes que la forman: neurona, sinapsis neuronal, etc. Además, se cubrirán tipos de redes neuronales, partiendo desde el perceptrón. Las definiciones y teoremas aquí explicados están basados en los libros [1] y [2], además del artículo en [3], donde Cybenko demuestra el teorema de aproximación para cualquier red neuronal de una capa oculta.
Los cursos en línea “Intro to Deep Learning,” del Carnegie Mellon University, “Convolutional Neural Networks for Visual Recognition,” del Stanford University School of Engineering, “Neural Networks,” de 3 blue 1 brown, y “Machine Learning Reading Group,” del KTH Royal Institute of Technology, también fueron de utilidad para esta investigación.
Este trabajo fue motivado por un interés que tuve en el Machine Learning para las artes visuales, por ahí de septiembre de 2018, y que culminó en una tesis de licenciatura en síntesis de textura donde el texto figuraría, pero se tuvo que quitar. Sin embargo, por cuatro primordiales razones me parece apropiado subir este contenido al sitio:
- Es un tema de actual relevancia, y que muy seguramente seguirá siendo una referencia para mí, particularmente para mí. Pero si tú llegas a emplearlo también, me dará gusto saberlo. Y si en algo de ello obtengo crédito, será aún mejor.
- Es un material que ya fue comentado y parcialmente corregido por mi tutor de tesis y sinodales.
- Es una recopilación de varios libros y cursos, enfocada en dar definiciones precisas, así como pretendí explicar con peras y manzanas cómo fueron evolucionando las redes neuronales en el curso de los años, qué problemas resuelven y por qué son útiles para el procesamiento de imágenes; así que puede servir como tutorial para introducirse en el tema.
- El material, más que referirse a problemas abiertos de matemáticas, es de uso público, y su belleza radica más en cómo se enseña o se discute.
Definición de red neuronal artificial
Una red neuronal artificial es un modelo computacional, inspirado en las redes neuronales humanas, que se utiliza para resolver una amplia variedad de tareas que son difíciles para la denominada “programación estructurada”. Su invención data del año 1943; la neurona de McCulloch-Pitts fue la primera neurona artificial. A esto le siguió el Perceptrón (1958), con un vector de entrada, una capa con una neurona oculta y una salida. Específicamente, las redes convolucionales son capaces de reconocer objetos en imágenes.
Las neuronas (o unidades de cálculo) son los bloques básicos de construcción de una red neuronal. Cada una de estas unidades tiene un número $k$ de conexiones de entrada (inputs) y puede tomar cierto número de estados. Piénsese, por ejemplo, en la red neuronal que reconoce dígitos del $0$ al $9$ a partir de imágenes. Entonces, por conexiones de entrada nos referimos a todos los pixeles de una imagen dada, y los posibles estados de la red son imágenes de dígitos $0$ al $9$, donde la red admite diversas caligrafías de los números, así como imágenes rotadas o desplazadas de los dígitos. Una imagen de un $6$ en la caligrafía Helvetica representaría un estado diferente al que describiría la imagen del mismo número, pero en caligrafía Comic Sans.
Para cierto estado descrito por un vector de entrada $\overrightarrow{x} = (x_0, x_1, \ldots, x_k)$ y por $W \in \mathcal{M}_{m\times n}(\mathbb{R})$, la neurona produce como salida una activación $g( \overrightarrow{x} ,W)$, donde $g: \mathbb{R}^p\times\mathbb{R}^{m\times k} \longrightarrow \mathbb{R}$ es una función fija, y $p = k+1$. Para facilitar la notación, podemos denotar $g( \overrightarrow{x} ,W) = g_W( \overrightarrow{x} )$, donde, para cada $W$, $g_W: \mathbb{R}^p \longrightarrow \mathbb{R}$ es la función que una neurona evalúa, dados los datos de entrada $ \overrightarrow{x} $ (esta definición se encuentra en [1], página 2).
En otras palabras, para una sóla neurona, el vector $W$ es una matriz de tamaño $1\times p$, que se puede visualizar así:

Y si hay $m$ neuronas, entonces $W$ es una matriz de $m \times k$ entradas, donde la activación $g( \overrightarrow{a}^{\text{ }0}, W)$, para esa capa con $m$ neuronas es:
\begin{align}
g \begin{pmatrix} \begin{bmatrix}{w_{0,0}}&{w_{0,1}}&\cdots & {w_{0,k}} \\ {w_{1,0}}&{w_{1,1}}&\cdots &{w_{1,k}} \\ \vdots &\vdots &\ddots &\vdots \\ {w_{m,1}}&{w_{m,2}}&\cdots &{w_{m,k}}
\end{bmatrix}
\begin{bmatrix} {a_0^{(0)}} \\ {a_{1}^{(0)}} \\ \vdots \\ {a_{k}^{(0)}} \end{bmatrix} +
\begin{bmatrix} {b_0^{(0)}} \\ {b_{1}^{(0)}} \\ \vdots \\ {b_{k}^{(0)}} \end{bmatrix} \end{pmatrix}
\text{,} \qquad \text{(1)}
\end{align}
donde bien podría $g$ ser un vector con $g_0, \ldots, g_m$ funciones de activación distintas, evaluando cada una de ellas a alguna de las $m$ neuronas de la capa $1$. Pero muy común es que una misma función de activación sea utilizada sobre todas las neuronas.
Equivalentemente, se puede escribir
\begin{align}
g \begin{pmatrix} \begin{bmatrix}{w_{0,0}}&{w_{0,1}}&\cdots &{w_{0,k}}&{b_{0, k+1}} \\ {w_{1,0}}&{w_{1,1}}&\cdots &{w_{1,k}}&{b_{1, k+1}}\\ \vdots &\vdots &\ddots &\vdots &\vdots\\ {w_{m,0}}&{w_{m,1}}&\cdots &{w_{m,k}}&{b_{m,k+1}}
\end{bmatrix}
\begin{bmatrix} {a_0^{(0)}} \\ {a_{1}^{(0)}} \\ \vdots \\ {a_{k}^{(0)}} \\ {1} \end{bmatrix}
\end{pmatrix}
\text{,} \qquad \text{(2)}
\end{align}
que tal vez llegaría a facilitar la programación de los datos.
Existen muchos tipos de redes neuronales: profundas, recurrentes, convolucionales, autoencoders, perceptrones multicapa, etc. Lo más pertinente sería encontrar una manera de “ir construyéndolas desde lo más simple posible, e ir entendiendo a ciertas redes como variantes de otras ya estudiadas. Finalmente, poder descartar algunas redes que no conciernen a nuestros objetos de estudio.” Así que mis textos sólo tomarán en cuenta, primero los casos más sencillos de red neuronal (perceptrón y perceptrón multicapa), y, ya que las redes convolucionales son aquéllas aplicables al modelo de síntesis de textura de interés, y éstas son un subconjunto de las redes neuronales profundas, lo que más nos interesa llegar a definir matemáticamente, es a la red neuronal profunda. Así,
Definición. Sean $E_i$ y $H_i$, con $i \in [L+1]$, espacios con producto interior. Una red neuronal profunda de $L$ capas es la composición de $L$ funciones $f_i: E_i \times H_i \longrightarrow E_{i+1}$ (ver (3)). Referiremos a las variables $x_i \in E_i$ como las variables de estado, mientras que las variables $\theta_i \in H_i$ son los parámetros. Es decir, si entendemos a $f_i$ como una función que va de $E_i$ en $E_{i+1}$ y que depende de $\theta_i \in H_i$, denotamos, para ciertos datos de entrada $x \in E_1$ a: $$ F: E_1\times (H_1 \times \ldots \times H_L) \longrightarrow E_{L+1}$$ tal que
\begin{align}
F(x, \theta) = (f_L \circ \ldots \circ f_1)(x)\text{,} \qquad \quad \text{(3)}
\end{align} donde cada $f_i$ depende del parámetro $\theta_i \in H_i$ y $\theta$ representa el conjunto de parámetros ${\theta_1, \ldots , \theta_{L}}$. ¡La función $F$ representa a la red neuronal completa!
Observamos que la notación suprimió el hecho de que una dada función $f_i$ depende del parámetro $\theta_i$, simplemente para facilitar la escritura.
En el caso de mis dibujos de redes neuronales (Figuras 1 y 2), así como para entender el modelo estudiado, consideraré que los estados $ \overrightarrow{x}^{\text{ }(0)}, \ldots , \overrightarrow{x}^{\text{ }(L)}$ son vectores real-valuados y que cada $\theta_k$ se conforma de un bias $ \overrightarrow{b_k}$, además de las entradas $w_{ij}$ de una matriz $W_k \in \mathcal{M}{m\times n}(\mathbb{R})$. El bias $ \overrightarrow{b_k} $ y las entradas $w_{ij} \in W_k$ son todos los parámetros de $\theta_k$ (ver (1)).
Si no se entendió esta explicación, vuelva a la Figura 1, e intente corroborar la notación con cada uno de los elementos de la ilustración. Luego inspeccione la Figura 2. De suma importancia resultaría hacer corresponder (mentalmente) la ilustración de una red neuronal profunda con su expresión algebraica. Por favor permanezca estudiando esta entrada de blog hasta que esto quede claro como el agua.
Note que, en la definición de red neuronal profunda, para $E_i$ se tiene que $i \in \{0, \ldots , L+1\}$ pues la cuenta empieza en cero (a la capa cero a veces ni siquiera se le llama capa) y el contradominio de $F$ siempre es “la capa que le sigue a $L$.”
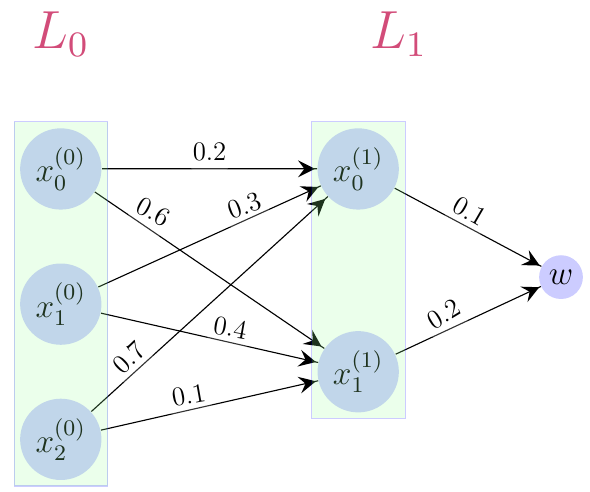
En particular, a un vector de entrada de una red, también se le puede denotar por $ \overrightarrow{x} $. Al escribir $ \overrightarrow{x}^{\text{ }(0)}, \ldots , \overrightarrow{x}^{\text{ }(L)}$, facilitamos la visualización de una red neuronal en un dibujo (ver Figura 2), donde los superíndices indican en qué capa de la red estamos y para la que $ \overrightarrow{x}^{\text{ }(k)} = (x_0^{(k)}, x_1^{(k)}, \ldots , x_n^{(k)})$; pero al escribir $ \overrightarrow{x} $ (o simplemente $x$), la lectura de las fórmulas se vuelve menos engorrosa. Usaremos la notación $L_i$, con $i \in \{0, \ldots , L+1 \}$, para esquematizar una capa específica de la red (ver Figura 2). En muchos textos, no se considera que el vector de entrada $x^{(0)}$ sea una capa de neuronas y bajo tal criterio, únicamente a las capas ocultas se les llama capas. En ese caso bastaría con especificar que $i \in \{1, \ldots , L+1 \}$, pero también complicaría un poquito la definición dada, de red neuronal profunda. A continuación dibujamos una red, donde $L_0$ representa la “capa” que tiene al vector de entrada:
Conclusiones
La definición matemática de red neuronal profunda es bonita porque encierra nociones de cálculo de varias variables, a pesar de que sea simple de entender. Bien pudiera servir como regla mnemotécnica para estudiar más cálculo o análisis matemático; se verá que el teorema de aproximación de redes neuronales usa la integral de Lebesgue, el teorema de Hahn Banach y el teorema de Representación de Riesz para su demostración.
No importa cuán sencilla o complicada sea la implementación de cierta red neuronal profunda, la definición que hemos dado sirve para representarla.
Bibliografía
[1] Martin Anthony. Discrete mathematics of neural networks: selected topics. SIAM, 2001.
[2] Anthony L Caterini and Dong Eui Chang. Deep Neural Networks in a Mathematical Framework. Springer, 2018.
[3] George Cybenko. Approximation by superpositions of a sigmoidal function. Mathematics of control, signals and systems, 2(4):303–314, 1989.
